Solving Towers of Hanoi with TLA+

Recently I’ve been reading Leslie Lamport’s Specifying Systems book. It’s free to read online, but I bought the hardcopy as I’m old fashioned like that.

Ever since I discovered TLA+, I’ve been fascinated with the idea of using precise language to describe systems upfront. Often as developers we either don’t do any upfront specification and just hope to wing it, or we very imprecisely add comments to our code as we go.

TLA+ gives you the language of mathematics (mostly numbers, sets, logic) to write your specs in and then provides the tools to check that your specifications actually work.

I think I’m going to write a more complete introduction to TLA+ in a later post but I wanted to share my first real (albeit very, very trivial) success with TLA+ in finding the shortest solution to the classic Towers of Hanoi problem for N discs.

I’ll walk through my spec, bit-by-bit. First we do some setup. We’ll be using sequences to represent the 3 stacks of discs and integers to represent the disc sizes:

EXTENDS Sequences, Integers
VARIABLE A, B, C

Next let’s describe the intitial state of our world. This is pretty straightforward, we have all discs on stack A. The smaller integers represent smaller discs:

Init == /\ A = <<1,2,3,4,5>>
        /\ B = <<>>
        /\ C = <<>>

Next we describe the Next state condition of the system. Which is a possibility of the top disc of any stack moving to any of the others (if allowed by the rules), we’ll use a procedure to represent this:

Next == \/ Move(A,B,C) \* Move A to B
        \/ Move(A,C,B) \* Move A to C
        \/ Move(B,A,C) \* Move B to A
        \/ Move(B,C,A) \* Move B to C
        \/ Move(C,A,B) \* Move C to A
        \/ Move(C,B,A) \* Move C to B

I’m sure this could be written more elegantly but I’m very new to TLA+, if you know a way please comment below. Now we need to write the Move(x,y,z) formula. This will move from x to y if allowed and leave z unchanged. We’ll use another procedure to represent whether the move can occur called CanMove(x,y):

Move(x,y,z) == /\ CanMove(x,y)
               /\ x' = Tail(x)
               /\ y' = <<Head(x)>> \o y
               /\ z' = z

CanMove written in English would say:

If the number of discs on x is zero, false. If the number of discs on y is greater than zero the answer is whether the head of stack y is greater than the head of stack x, otherwise it’s true

The way I wrote this in TLA+ is:

CanMove(x,y) == /\ Len(x) > 0
                /\ IF Len(y) > 0 THEN Head(y) > Head(x) ELSE TRUE

Now this system can quite happily continue forever, but we want to stop it in the winning position (all discs on Rod A). We can write an invariant (state that should never happen) and specify this to the TLA+ model checker software, which will give us an error trace (set of moves) when this condition occurs. We’ll get the shortest path to the Invariant condition as the model checker does a breadth-first search of the decision tree.

Here’s the invariant, our winning condition:

Invariant == C /= <<1,2,3,4,5>>

Here’s the Model checker’s error trace to our solution:

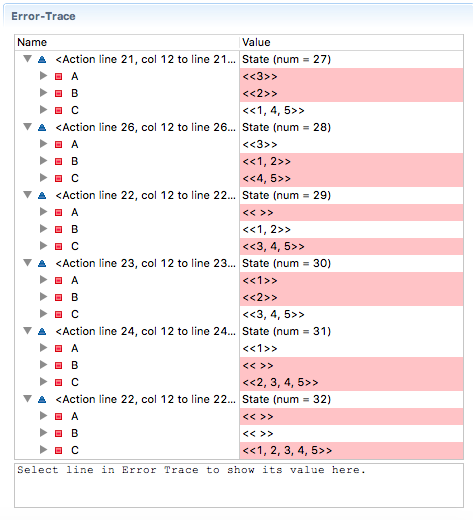
We see for a 5 stack Hanoi problem it took 31 steps (it says 32 because it counts the initial state), which fits with the rule of 2^n - 1 steps.

Here’s the full spec once pretty printed by LaTeX:

and in ASCII:

------------------------------- MODULE Hanoi -------------------------------

EXTENDS Sequences, Integers
VARIABLE A, B, C


CanMove(x,y) == /\ Len(x) > 0
                /\ IF Len(y) > 0 THEN Head(y) > Head(x) ELSE TRUE

Move(x,y,z) == /\ CanMove(x,y)
               /\ x' = Tail(x)
               /\ y' = <<Head(x)>> \o y
               /\ z' = z

Invariant == C /= <<1,2,3,4,5>>   \* When we win!

Init == /\ A = <<1,2,3,4,5>>
        /\ B = <<>>
        /\ C = <<>>

Next == \/ Move(A,B,C) \* Move A to B
        \/ Move(A,C,B) \* Move A to C
        \/ Move(B,A,C) \* Move B to A
        \/ Move(B,C,A) \* Move B to C
        \/ Move(C,A,B) \* Move C to A
        \/ Move(C,B,A) \* Move C to B
=============================================================================